geom.f File Reference

Basic geometrical calculations. More...

Go to the source code of this file.

Functions/Subroutines
real(gridman_dp) function	gridman_triaarea (X1, Y1, X2, Y2, X3, Y3)
	Area of a triangle.
real(gridman_dp) function	gridman_triavol (X1, Y1, X2, Y2, X3, Y3)
	Volume of the solid of revolution obtained by rotating of a triangle around axis X=0.
real(gridman_dp) function	gridman_dist2d (X1, Y1, X2, Y2)
	Distance between two points on a plane.
subroutine	gridman_norm2d (X0, Y0, XN, YN)
	Vector (XY,YN) normal to (X0,Y0)
real(gridman_dp) function	gridman_conarea (X1, Y1, X2, Y2)
	Area of the conical surface obtained by rotation of the interval (X1,Y1),(X2,Y2) around X=0.
logical function	gridman_cross2d (X0, Y0, V, U, X1, Y1, X2, Y2, XI, YI)
	Intersection of "particle trajectory" with an interval (2D) More...
logical function	gridman_intersect2d (X11, Y11, X12, Y12, X21, Y21, X22, Y22, XI, YI)
	Intersection of two intervals on a plane. More...
logical function	gridman_point_in_polygon (XP, YP, NP, X0, Y0)
	Find if point lies inside a closed polygon. More...
logical function	gridman_close2interval2d (X1, Y1, X2, Y2, X, Y, TOL)
	Find if point is close to the interval within prescribed tolerance. More...

Detailed Description

Basic geometrical calculations.

Definition in file geom.f.

Function/Subroutine Documentation

logical function gridman_cross2d	(	real(gridman_dp), intent(in)	X0,
		real(gridman_dp), intent(in)	Y0,
		real(gridman_dp), intent(in)	V,
		real(gridman_dp), intent(in)	U,
		real(gridman_dp), intent(in)	X1,
		real(gridman_dp), intent(in)	Y1,
		real(gridman_dp), intent(in)	X2,
		real(gridman_dp), intent(in)	Y2,
		real(gridman_dp), intent(out)	XI,
		real(gridman_dp), intent(out)	YI
	)

Intersection of "particle trajectory" with an interval (2D)

Find a point where a "particle" with velocity (VX0,VY0) which starts from point (X0,Y0) intersects the interval [(X1,Y1)(X2,Y2)]. The function returns .TRUE. if intersection exist and .FALSE. otherwise

Parameters

[in]	x0	X-coordinate of the "particle" starting point
[in]	y0	Y-coordinate of the "particle" starting point
[in]	v	X-component of the particle velocity
[in]	u	Y-component of the particle velocity
[in]	x1	X-coordinate of the first end of the interval
[in]	y1	Y-coordinate of the first end of the interval
[in]	x2	X-coordinate of the second end of the interval
[in]	y2	Y-coordinate of the second end of the interval
[out]	xi	X-coordinate of the intersection point
[out]	yi	Y-coordinate of the intersection point

Definition at line 108 of file geom.f.

References gridman::gridman_dp.

Referenced by find_closest_boundary().

Here is the caller graph for this function:

logical function gridman_intersect2d	(	real(gridman_dp), intent(in)	X11,
		real(gridman_dp), intent(in)	Y11,
		real(gridman_dp), intent(in)	X12,
		real(gridman_dp), intent(in)	Y12,
		real(gridman_dp), intent(in)	X21,
		real(gridman_dp), intent(in)	Y21,
		real(gridman_dp), intent(in)	X22,
		real(gridman_dp), intent(in)	Y22,
		real(gridman_dp), intent(out)	XI,
		real(gridman_dp), intent(out)	YI
	)

Intersection of two intervals on a plane.

Find intersection point of two intervals on a plane. The function returns .TRUE. if intersection exist and .FALSE. otherwise

Parameters

[in]	x11	X-coordinate of the first end of the first interval
[in]	y11	Y-coordinate of the first end of the first interval
[in]	x12	X-coordinate of the second end of the first interval
[in]	y12	Y-coordinate of the second end of the first interval
[in]	x21	X-coordinate of the first end of the second interval
[in]	y21	Y-coordinate of the first end of the second interval
[in]	x22	X-coordinate of the second end of the second interval
[in]	y22	Y-coordinate of the second end of the second interval
[out]	xi	X-coordinate of the intersection point
[out]	yi	Y-coordinate of the intersection point

Definition at line 167 of file geom.f.

References gridman::gridman_dp.

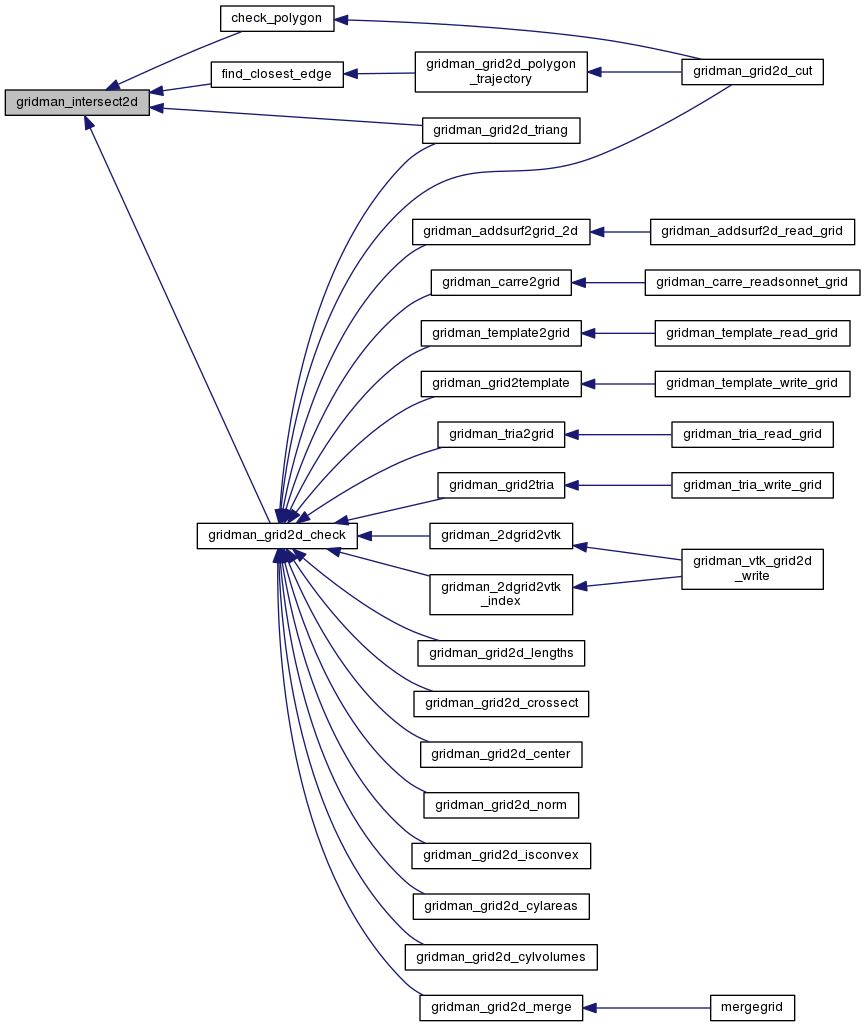
Referenced by check_polygon(), find_closest_edge(), gridman_grid2d_check(), and gridman_grid2d_triang().

Here is the caller graph for this function:

logical function gridman_point_in_polygon	(	real(gridman_dp), dimension(np)	XP,
		real(gridman_dp), dimension(np)	YP,
		integer(gridman_sp), intent(in)	NP,
		real(gridman_dp)	X0,
		real(gridman_dp)	Y0
	)

Find if point lies inside a closed polygon.

The function returns .TRUE. if the point (X0,Y0) lies inside the polygon (XP,YP) and .FALSE. otherwise

It is assumed that the polygon is simple and closed. That is, no intesection between polygon edges, first and last vertex of the polygon are the same.

WARNING: this function does not check that the polygon is simple and closed

Crossing number method - even-odd test - is applied

Parameters

[in]	np	Number of the polygon vertices - first and last vertex is counted twice
	xp	X-coordinates of the vertices
	yp	Y-coordinates of the vertices
	x0	X-coordinate of the point to be checked
	y0	Y-coordinate of the point to be checked

Definition at line 259 of file geom.f.

References gridman::gridman_dp, gridman::gridman_sp, and gridman::gridman_tol.

Referenced by find_closest_boundary(), and gridman_grid2d_cut().

Here is the caller graph for this function:

logical function gridman_close2interval2d	(	real(gridman_dp), intent(in)	X1,
		real(gridman_dp), intent(in)	Y1,
		real(gridman_dp), intent(in)	X2,
		real(gridman_dp), intent(in)	Y2,
		real(gridman_dp), intent(in)	X,
		real(gridman_dp), intent(in)	Y,
		real(gridman_dp), intent(in)	TOL
	)

Find if point is close to the interval within prescribed tolerance.

Function returns .TRUE. if the point (X,Y) lies on the interval [(X1,Y1),(X2,Y2)]) withing relative tolerance TOL and .FALSE. otherwise

Parameters

[in]	x1	X-coordinate of the 1st end of the interval
[in]	y1	Y-coordinate of the 1st end of the interval
[in]	x2	X-coordinate of the 2nd end of the interval
[in]	y2	Y-coordinate of the 2nd end of the interval
[in]	x	X-coordinate of the point to be checked
[in]	y	Y-coordinate of the point to be checked
[in]	tol	Tolerance parameter which defines relative accuracy, e.g. 1e-7

Definition at line 325 of file geom.f.

References gridman::gridman_dp.

Referenced by check_polygon().

Here is the caller graph for this function: